Mathematics, the universal language of the universe, is a treasure trove of formulas, equations, and concepts. Among these mathematical jewels, the A3+B3 formula, also known as the sum of cubes, shines brightly as an enigmatic and intriguing algebraic expression. In this comprehensive article, we embark on a journey to delve deep into the realms of this mathematical marvel. We will explore its historical roots, the core of its algebraic identity, the vast spectrum of its applications, and its enduring significance in the world of mathematics.
What is the A3+B3 Formula?
The A3+B3 formula, a seemingly simplistic yet profoundly captivating mathematical expression, symbolizes the sum of two cubes, each represented by the variables A and B. This algebraic gem can be distilled to its most fundamental form:
The essence of this expression lies in its representation of the third power of two distinct real numbers, A and B. The act of adding and yields a result that, despite its apparent simplicity, resonates throughout the mathematical cosmos.
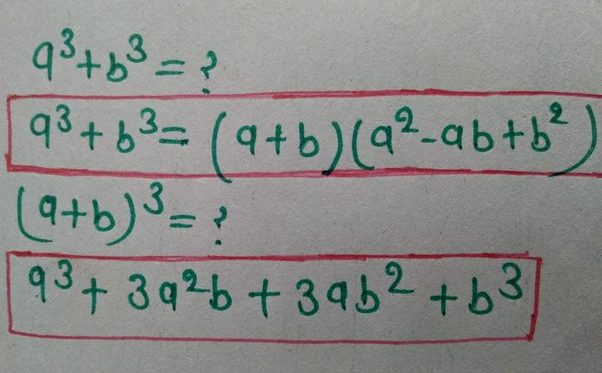
History of the A3+B3 Formula
The origins of the A3+B3 formula are deeply rooted in the annals of mathematical history, with ancient luminaries such as Diophantus and Fermat laying the foundation for its exploration. However, it was the brilliant Swiss mathematician Leonhard Euler who made remarkable contributions in the 18th century. Euler’s work not only shed light on the formula but also initiated the journey towards a comprehensive understanding of its applications and implications.
Understanding the Algebraic Expression
To unlock the secrets of the A3+B3 formula, we must dissect it:
- and are tangible, real numbers, each with its unique value.
- signifies the cube of .
- signifies the cube of .
The act of adding and results in the sum of these cubes. This deceptively straightforward expression serves as the gateway to a profound mathematical world where the properties of cubes intertwine and offer a deeper understanding of their interactions, igniting the spark of mathematical curiosity.
Practical Applications
The versatility of the A3+B3 formula extends across diverse mathematical landscapes. It becomes a valuable tool in algebraic manipulations, number theory, and even the intriguing realm of cryptography. In certain cases, it serves as a cornerstone for solving intricate equations, its influence rippling through the mathematical universe.
A3+B3 in Geometry
Geometry, a realm of shapes, sizes, and spatial dimensions, isn’t exempt from the allure of the A3+B3 formula. This formula finds a natural home in solving problems related to volume. As the cube of a number often signifies a three-dimensional space, geometric calculations, and the exploration of various shapes benefit significantly from its application.
Variations and Expansions
The ever-evolving nature of mathematics fuels the exploration of variations and expansions of the A3+B3 formula. Mathematicians, driven by curiosity, have unleashed their creativity to introduce complexities and depth, unearthing new dimensions of its applications. Some of these variations have paved the way for groundbreaking discoveries.
Simplifying the Formula
While the A3+B3 formula may seem daunting at first glance, the mathematical community has not left it shrouded in complexity. Various methods have been devised to simplify the formula, rendering it more accessible for solving equations and addressing mathematical problems. These simplifications are essential for practical applications and widespread adoption.
A3+B3 in Real Life Problems
The A3+B3 formula, often seen as an abstract mathematical concept, demonstrates its real-world relevance. From engineering to physics, its application contributes to the resolution of practical challenges involving cubic quantities. This bridge between the abstract and the concrete underscores its pragmatic importance.
A Mathematical Insight
The A3+B3 formula, while outwardly appearing as a straightforward addition, conceals a profound mathematical insight. It transcends the mere act of combining numbers; it invites mathematicians to explore the properties of cubes and their intricate interactions. Its enigma continues to captivate mathematicians and propel them towards uncharted mathematical territories.
Importance in Modern Mathematics
In the contemporary landscape, the A3+B3 formula retains its status as a fundamental concept in mathematics. Its applications have expanded beyond traditional boundaries, permeating fields such as computer science and cryptography. Its significance in modern mathematics cannot be overstated, underscoring its relevance in the digital age.
Fun with A3+B3
In the world of mathematics, fun and fascination often go hand in hand. Exploring the A3+B3 formula unlocks a treasure chest of engaging puzzles and brain teasers. These challenges provide an enjoyable platform for students and enthusiasts to test their mathematical prowess while fostering a love for the subject.
Must Read:
Challenges and Complexities
However intriguing the A3+B3 formula may be, it does not come without its share of challenges. Some mathematical problems related to this formula can be highly intricate, demanding advanced mathematical techniques and innovative approaches to conquer. These challenges, while daunting, serve as beacons guiding mathematicians towards new horizons.
Conclusion
In conclusion, the A3+B3 formula, with its simplicity and profound implications, stands as a testament to the timeless allure of mathematics. From its humble historical origins to its modern applications, this algebraic gem has continued to be a source of fascination and inspiration in the mathematical realm.

